سنتعلم في هذا الدرس كيفية إيجاد نظيم شعاع أو مايُعرف ب طول الشعاع مع إعطاء أمثلة تطبيقية على ذلك وحلها.
ماهو الشعاع في الرياضيات:
١. المبدأ:أي نقطة البداية
٢.الجهة: مثلاً الشعاع AB جهته من A إلى B أو من B إلى A
٣.الطول: أي قياس الطول بالسنتيمتر أو الميليمتر أو… الخ.
قانون طويلة الشعاع:
في معلم متجانس (o, i, j) لدينا الشعاع
(u( x،y
أي ان فاصلته على المحور ox هي x، وترتيبه على المحور oy هو y
فإنّ قانون طويلة الشعاع u هي:
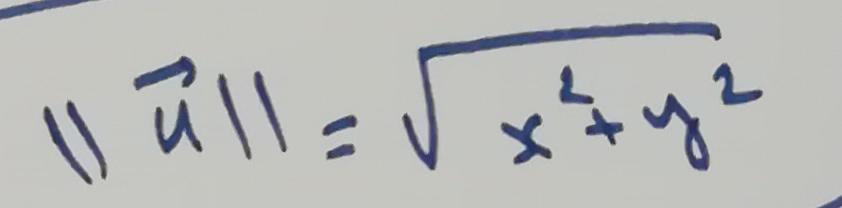
مثال:

الحل:
الطلب الأول:
لنوجد نظيم كل شعاع على حدى أولاً لنوجد نظيم الشعاع AB،إن للشعاع AB نقطتين فيجب علينا إيجاد فاصلة الشعاع وترتيبه في القانون السابق
الفاصلة هي فرق فاصلتيA وB والترتيب هي فرق ترتيب النقطتين A و B فيصبح القانون بالشكل:
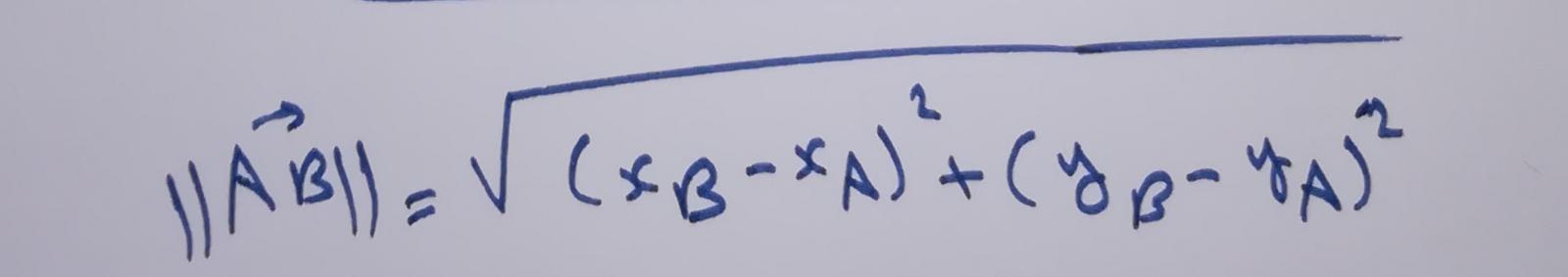
نعوّض بالاحداثيات المعطاة في نص المسألة فنجد:
نجمع الحدود المتشابهة اي الأعداد الصحيحة مع الاعداد الصحيحة والجذور مع الجذور إن وجدت فنجد العلاقة أصبحت بالشكل الآتي:
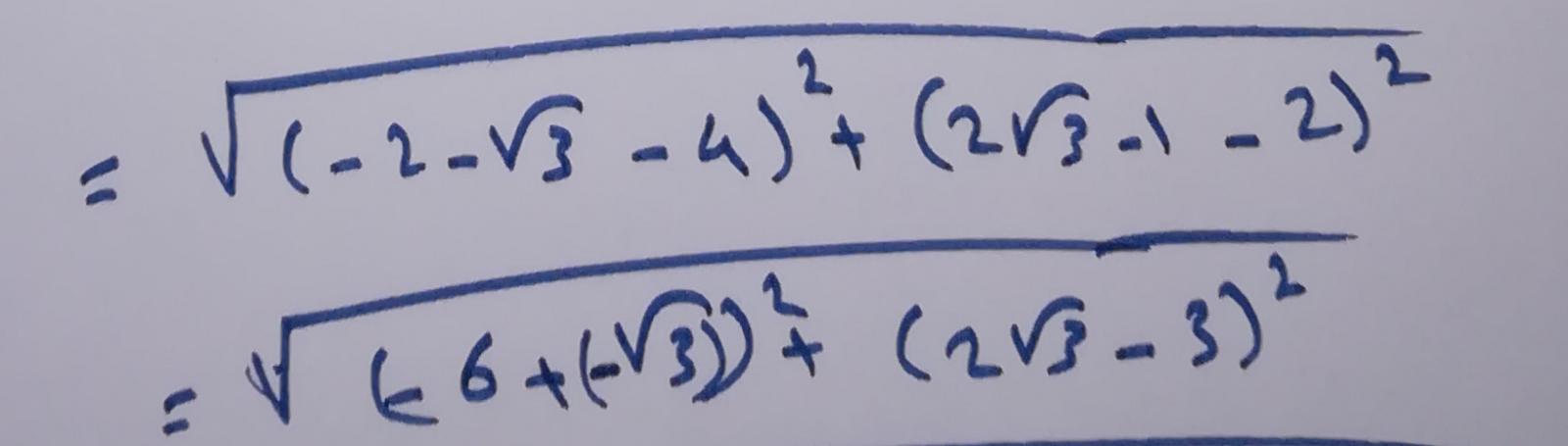
نفك المطابقات التربيعية الموجودة تحت الجذر ونجمع الحدود المتشابهة فنجد:
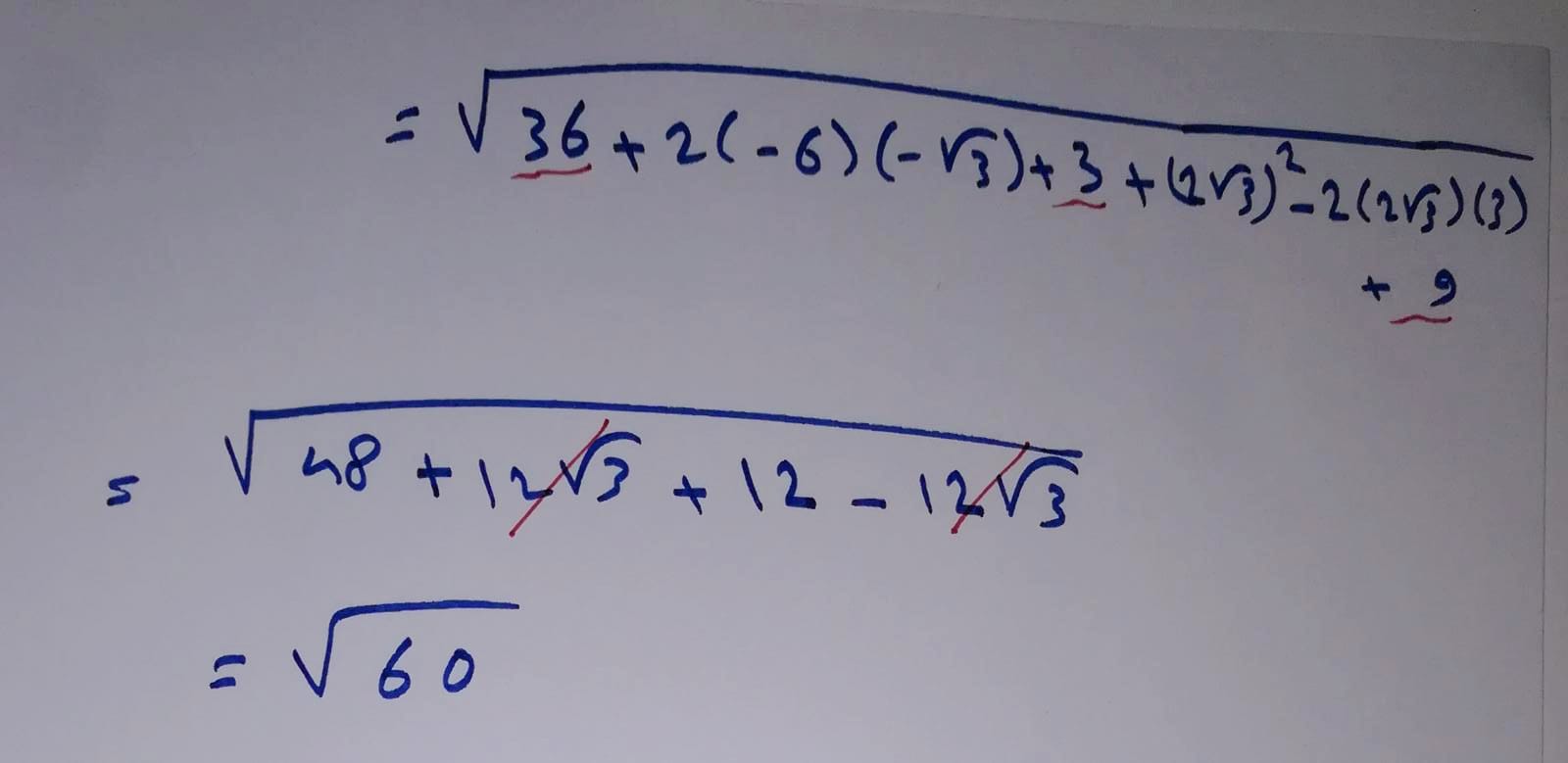
- بنفس الطريقة نوجد نظيم الشعاعAC:
- نعوّض بالاحداثيات المعطاة في نص المسألة.
- نجمع الحدود المتشابهة اي الأعداد الصحيحة مع الأعداد الصحيحة والجذور مع الجذور إن وجدت.
- نفك المطابقات التربيعية الموجودة تحت الجذر ونجمع الحدود المتشابهة فنجد:
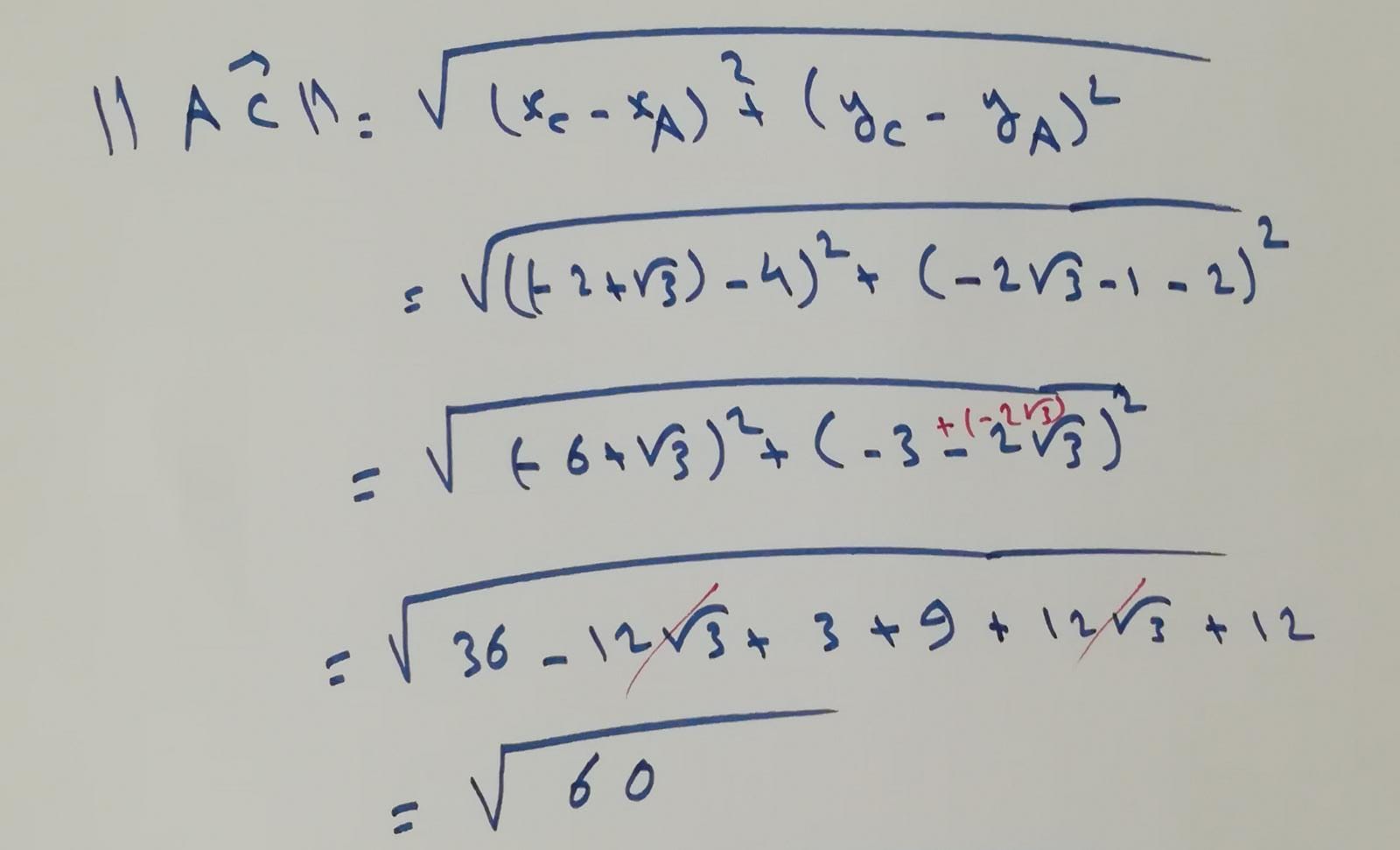
- نوجد نظيم الشعاع BC:
- نعوّض بالاحداثيات المعطاة في نص المسألة.
- نجمع الحدود المتشابهة اي الأعداد الصحيحة مع الاعداد الصحيحة والجذور مع الجذور.
- نربع الأعداد ونجمعها لنجد الناتج النهائي:
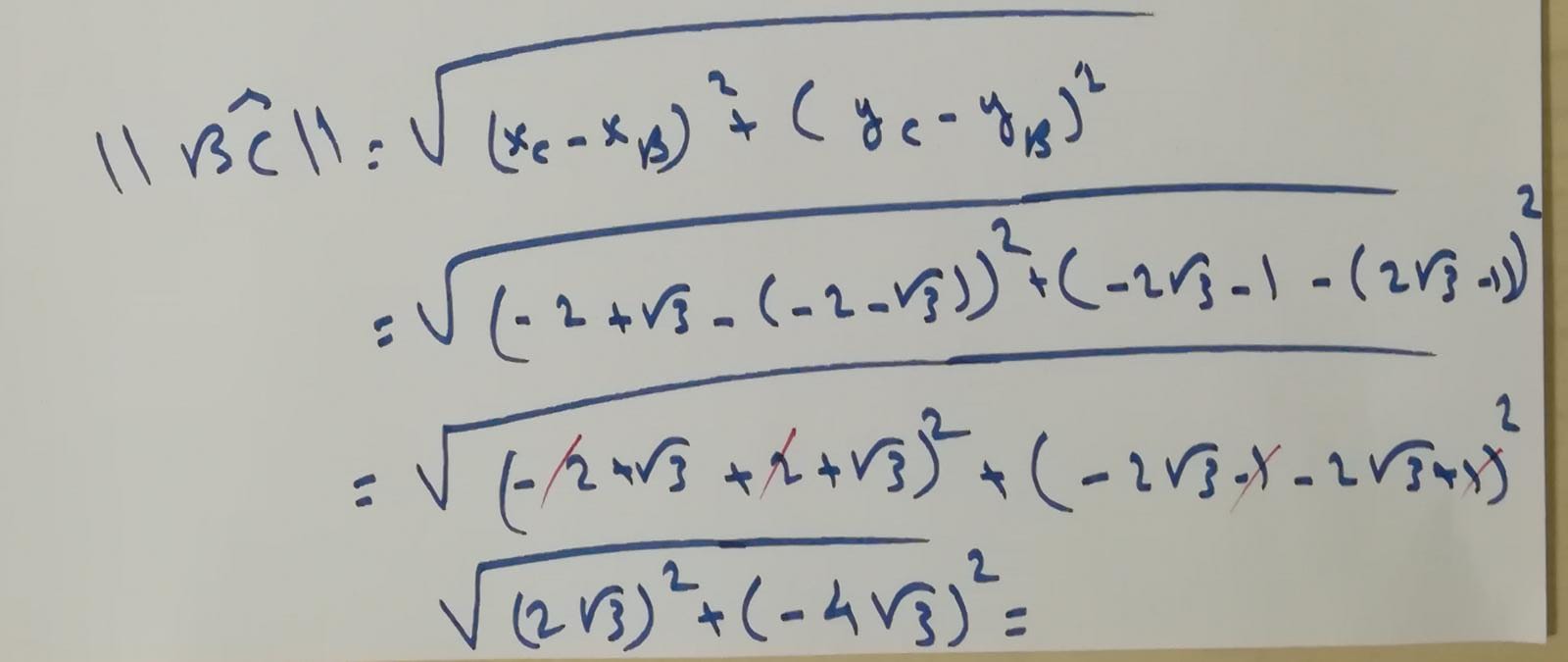
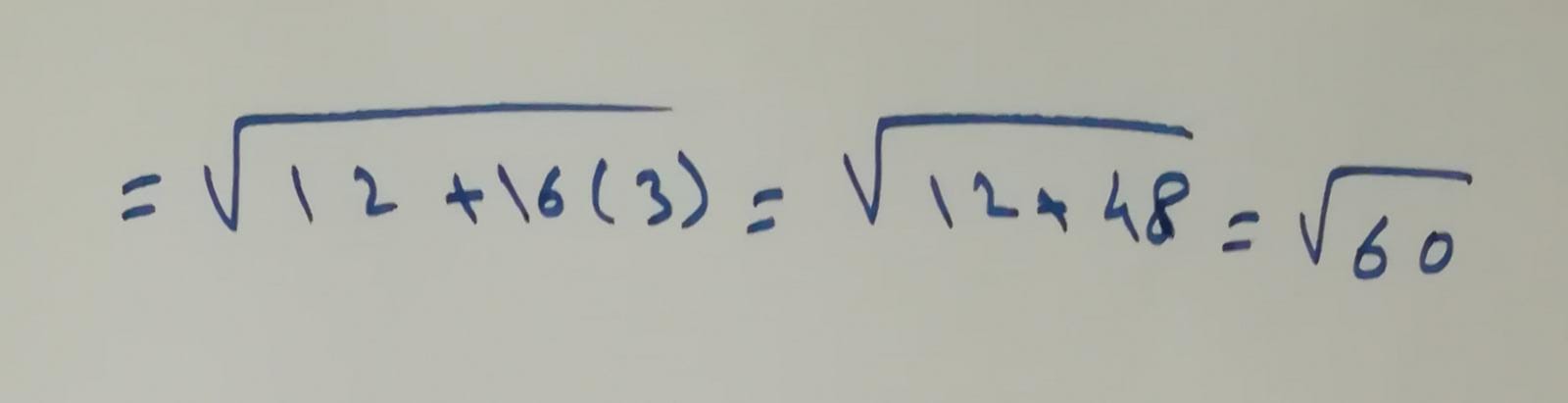
الطلب الثاني:
نلاحظ أن أطوال الأضلاع الثلاثة متساوية وكلها تساوي جذر ال60 إذاً ومنه نستنتج أنّ المثلث متساوي الأضلاع.
ولمزيد من الفائدة إليكم هذا الفيديو:


مشكورين درس مفهوم 💜💜