العمليات على التوابع (جمعها ،طرحها، ضربها ، قسمتها) وإيجاد مجموعات التعريف لكل منها
سنتعرف في هذا المقال على بعض العمليات على التوابع (جمعها ،طرحها، ضربها قسمتها) وسنتعلم كيفية إيجاد مجموعات التعريف لكل من هذه العمليات.
أولاً: (جمع التوابع)
ليكن لدينا تابعان F(x) ،g(x) معرفان على مجموعتي التعريف Df , Dg على التوالي عندئذٍ:
يرمز لجمع هذين التابعين ب : f+g
تعريفهما : F(x) +g(x)
مجموعة تعريف مجموع هذين التابعين هي :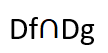
أي أن مجموع تعريف جمع التابعين هي المجموعة الناتجة عن تقاطع مجموعتي التعريف لكل منهما.
ثانياً: ( طرح التوابع)
ليكن لدينا تابعان F(x) ،g(x) معرفان على مجموعتي التعريف Df , Dg عندئذٍ:
رمز جمع هذين التابعين : f-g
تعريفهما : F(x) – g(x)
مجموعة تعريف طرح التابعين هي :
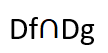
أي أن مجموع تعريف طرح التابعين هي المجموعة الناتجة عن تقاطع مجموعتي تعريفهما
ثالثاً: ( ضرب التوابع)
ليكن لدينا تابعين F(x) ،g(x) معرفان على مجموعتي التعريف Df , Dg عندئذٍ:
رمز ضرب هذين التابعين :
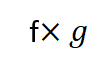
تعريفهما :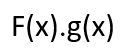
مجموعة تعريف ضرب التابعين هي :
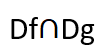
أي أن مجموع تعريف ضرب التابعين هي المجموعة الناتجة عن تقاطع مجموعتي تعريفهما
رابعاً: ( قسمة التوابع)
ليكن لدينا تابعان F(x) ،g(x) معرفان على مجموعتي التعريف Df , Dg عندئذٍ:
رمز قسمة هذين التابعين :
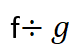
تعريفهما :
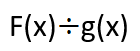
مجموعة تعريف قسمة التابعين هي :
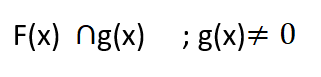
أي أن مجموع تعريف قسمة التابعين هي المجموعة الناتجة عن تقاطع مجموعتي تعريفهما، بشرط ألّا يكون المقام يساوي الصفر
لنعطي أمثلة على هذه العمليات :
مثال1:
لدينا التابعين f،g معرفان وفق:
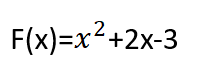
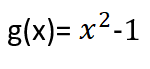
والمطلوب:
أوجد مجموعة تعريف كل من f ، g ، f+g، fg
ثم احسب: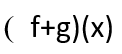 
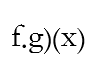
الحل:
_ إن كلاٌ من التابعين f،g هو تابع كثير حدود ( تابع صحيح )؛ لذا فإن مجموعة التعريف لكلاّ التابعين هي R ( مجموعة الأعداد الحقيقية ).
_ مجموعة تعريف مجموع التابعين هو تقاطع مجموعة تعريفهما أي : 
وإن تقاطع أي مجموعة مع نفسها هو المجموعة نفسها أي أن مجموعة تعريف مجموع التابعين هو R
_ وبنفس الطريقة نوجد مجموع تعريف جداء التابعين ( وهو تقاطع مجموعة تعريفهما) وهو R أيضاً
-لنوجد الآن :
مجموع التابعين :
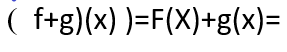
حيث أننا في الخطوة الأخيرة جمعنا الحدود المتشابهة.
جداء التابعين:
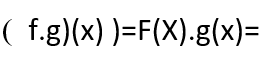
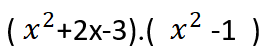
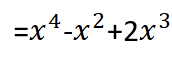
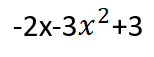
حيث أننا في الخطوة الأخيرة قمنا بنشر الأقواس ،ثمّ بجمع الحدود المتشابهة.
لمزيدٍ من الأمثلة والشرح المفصّل تابعوا هذا الفيديو: