سنتعلم في هذا الدرس من دروس الرياضيات تعريف النسبة، كيفية كتابة النسب وتحويلها إلى أبسط صورة، وكيفية كتابة النسب الموسعة مع تمارين على كافة هذه الأفكار.
النسبة: عبارة عن مقارنة كميتين باستخدام القسمة ،يمكن التعبير عن نسبة الكميتين a و b بالصورة a إلى b أو b : a أو a/b ، حيث 0 ≠ b .النسب يعبر عنها عادة بأبسط صورة.
نسبة البعدين 18:32 و 9:16 متساوية وذلك لأننا إذا قمنا باختزال الكسر 18/32 وذلك بتقسيم بسطه ومقامه على العدد 2 فإننا سنحصل على النسبة 9/16
ونكتبها بالشكل الرياضي بالشكل:
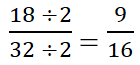
مثال على كتابة النسب وتحويلها إلى أبسط صورة:
الألعاب الرياضية: متوسط عدد النقاط لالعب السلة هو نسبة عدد الأهداف ذات
النقطتين إلى عدد الأهداف ذات الثالث نقاط. وقد ّ حقق عبد الله لاعب فريق الأهلي
أعلى متوسط للنقاط في في أحد المواسم الرياضية . إذا أحرز ّ عبد الله 521 ً هدفا ذو
ثالث نقاط و 181 هدفا ذو نقطتين، احسب متوسط ّ نقاط عبد الله.
الحل:
لإيجاد متوسط نقاط عبد الله يجب علينا أن نقسّم عدد الأهداف ذات النقطتين إلى عدد الأهداف ذات الثلاث نقاط ثمّ نجري عملية قسمة البسط على المقام ونكتب ذلك بشكل رياضي بالشكل:

وبإجراء عملية القسمة نحصل على العدد 0.347 وهو متوسط نقاط عبد الله
تمرين موجه:
يوجد في مدرسة أسامة الثانوية 190 معلماً و 2650 طالباً . مالنسبة التقريبية للطلاب إلى المعلمين في هذه المدرسة؟
الحل:
لإيجاد النسبة المطلوبة نقوم بكتابة نسبة عدد الطلاب على عدد المعلمين في المدرسة ثمّ نقوم بإختزال الكسر إن أمكن ذلك ونعبّر عن ذلك بالشكل:
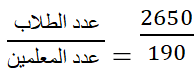
وبإجراء عملية القسمة نحصل على العدد 13.9 وهو النسبة التقريبية للطلاب إلى المعلمين.
النسب الموسعة:
النسب الموسعة: يمكن استخدامها لمقارنة ثلاث كميات أو أكثر
فالتعبير a:b:c يعني أن نسبة أول كميتين a:b ،ونسبة آخر كميتين هي b:c ،ونسبة الكمية الأولى والأخيرة هي a:c
مثال على استخدام النسب الموسعة:
اذا كانت النسبة بين قياسات زوايا مثلث هي 5 :4 :3 .فجـد قياسات الزوايا.
الحل:
نظراً لأن نسبة 3/4 أو 3:4 هي نفسها نسبة 3x/4x
إذاً يمكن كتابة النسبة الموسعة 5 :4 :3 بالشكل الآتي:
3x:4x:5x
ونحن نعلم أن مجموع قياسات أي مثلث تساوي 180 درجة ، لذلك نستطيع التعبير عن مجموع قياسات المثلث المعطى في هذا المثال بالعلاقة الآتية:
3x + 4x +5x =180
أصبح لدينا معادلة بمجهول واحد ، نقوم بحلها وذلك أولاً بجمع الحدود المتشابهة ( جمع أمثال ال x ) ثمّ بقسمة طرفي المعادلة على أمثال المجهول x وذلك بالشكل:
12x=180
x=15
الآن نعود إلى النسب المعطاة ونعوّض قيمة x بالعدد 15 فنحصل على قياسات الزوايا المطلوبة وذلك بالشكل الآتي:
قياس الزاوية الأولى:
45=(15)3x=3
قياس الزاوية الثانية:
60 =(15)4 =4x
قياس الزاوية الثالثة:
75 =( 15) 5 = 5x
للتحقق من صحة الحل نجمع قياسات المثلث الناتجة:
45+60+75=180
وبما أنّ الناتج 180 درجة إذاً فإنّ القياسات الناتجة صحيحة.
تمرين موجه:
في مثلث، تبلغ نسبة أطوال الأضلاع 3 : 2 : 2 ومحيطه يساوي 392 . ِ أوجد طول أطول ضلع بهذا المثلث
الحل:
بما أن نسبة الأطوال هي 2:2:3 فهي نفسها 2x:2x:3x
ونحن نعلم أن محيط أي مثلث هو مجموع أطوال أضلاعه ومنه فإنّ محيط المثلث المعطى هو:
2x+2x+3x=392
وهي معادلة بمجهول واحد نحلها وذلك بجمع أمثال المجهول x ثمّ بقسمة الطرفين على أمثال هذا المجهول فينتج:
7x=392
x=392/7
x=56
نعود الآن إلى المطلوب إيجاده في التمرين وهو إيجاد أطول أضلاع المثلث ، إنّ أطول أضلاع المثلث هو الضلع الذي يملك النسبة الأعلى أي هو النسبة 3x
نعوّض بقيمة x التي نتجت معنا وهي العدد 56 فينتج
168=(56)3x=3
وهو الضلع المطلوب

