تركيب تابعين (gof ،fog) وإيجاد مجموعة التعريف لكل منهما
بعد أن تعلمنا في مقال سابق القيام ببعض العمليات على التوابع وهي: (جمع التوابع ، طرحها ، ضربها ،قسمتها ) ، فإننا سنتابع في هذا المقال تعلم عملية جديدة على التوابع ألا وهي تركيب التوابع التي يرمز لها بالرموز ( gof ، fog ) وسنتعلم إيجاد مجموعة التعريف لكليهما.تعريف تركيب تابعين:
ليكن لدينا التابعين g، f . التابع gof يُقرأ: ” f ثمّ g ” أو ” g دائرة f “
وهو التابع المعرف بالعلاقة:
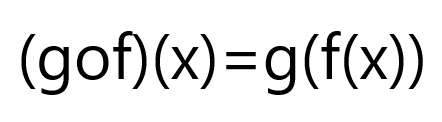
مثال:
ليكن f التابع المعرف على R بالعلاقة:
![]()
وليكن g التابع المعرف على ![]() بالعلاقة:
بالعلاقة:
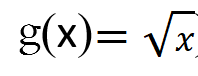
عندئذ:
أوجد gof، fog وهل : gof= fog
الحل:
أولاً : إيجاد gof
نكتب تعريف تركيب التابعين :
![]()
ثمّ نبدل بالتعريف التابع f(x) بقاعدة الربط المعطاة ونستكمل الحل فينتج:
g(x-2) =
ثم نستبدل بالتابع (x)g كل x ب x-2 فينتج:
![]() وهو الحل النهائي .
وهو الحل النهائي .
ثانياً: إيجاد fog
نكتب تعريف التابعين:![]()
![]() ثمّ نستبدل بالتابع f كل x بجذر ال x فينتج:
ثمّ نستبدل بالتابع f كل x بجذر ال x فينتج:
![]()
ثالثاً: هل gof= fog أم لا
نستنتج من الطلبين السابقين أن:
fog لايساوي gof
مثال2:
ليكن f ، g التابعين المعرفين بالعلاقتين:
![]()
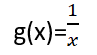
- احسب gof وعين مجموعة قيم x التي يكون عندها هذا الحساب ممكناً، أي مجموعة تعريف gof .
2.أعد السؤال في حالة fog.
الحل:
أولاً: إيجاد مجموعة تعريف gof
لإيجاد مجموعة تعريف gof نوجد مجموعة تعريف f ومجموعة تعريف g
إن f تابع صحيح ونحن نعلم أن مجموعة تعريف التابع الصحيح هي R
” مجموعة الأعداد الحقيقية”
إن g هو تابع كسري ونحن نعلم أن مجموعة تعريف التابع الكسري هي :
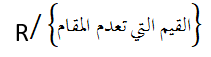
وفي هذا التابع ينعدم المقام عندما 0=X وبالتالي فإن مجموعة تعريف التابع g هي:
![]()
مجموعة تعريف gof هي نفسها مجموعة تعريف f مع الشرط الإضافي الموجود في التابع g وهو أن x لايساوي الصفر ولكن نستعيض عنه بأن:
f(x) لايساوي الصفر ولكننا نلاحظ أن f لايمكن أن يساوي الصفر لأنه ناتج عن مربع عدد حقيقي ” ومربع العدد الحقيقي دائماٌ موجب ” مضافاٌ إليه العدد الواحد الموجب وبالتالي فإن التابع f سيكون موجباٌ ولايمكن أن يساوي الصفر.
إذاٌ لا داعي للشرط الإضافي ، ولذلك نستنتج أن مجموعة تعريف gof هو R
ثانياٌ: حساب gof
نحل هذا الطلب بنفس الخطوات التي اتبعناها بالمثال السابق:
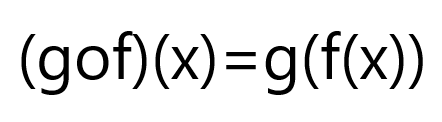
![]()
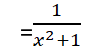
لمعرفة حل الطلب الثاني ولمزيد من الشرح والتوضيح شاهدوا الفيديو الآتي: