مجموعات تعريف بعض التوابع ( التابع الصحيح, التابع الكسري, التابع الجذري):

1.تابع كثير الحدود( التابع الصحيح):

قبل أن نتعرّف على مجموعة تعريف التابع الصحيح ، لنتعرف أولأ على شكله العام:

شكله العام من الشكل :

F(X)=Axⁿ+Bx^n-1+Cx^n-2+……..+K

عدد طبيعي Nأعداد حقيقية و العدد  A,B,C,….,K :حيث

أمثلة على بعض التوابع الصحيحة ( تابع كثير الحدود):

1. F(X)=3X²+4X+8g
2. F(X)=-5X^-3+4X^-1-7
3. F(y)=-8y+2

إنّ مجموعة تعريف جميع التوابع الصحيحة هي:

(R) مجموعة الأعداد الحقيقية

لنعد الآن إلى التوابع الثلاث السابقة ولنحل السؤال : أوجد مجموعة تعريف هذه التوابع

الحل: مجموعة التعريف هي

R

( ويرمز لمجموعة التعريف اختصاراٌ في بعض المناهج م.ت )

2‌. التابع الكسري

هو أي تابع يحوي على بسط ومقام شرط أن يكون في المقام متحول ( مجهول) أو أكثر ، أي أنه لايكفي أن يكون لدينا كسر بسطه يحوي متحولات ومقامه يحتوي على عدد مثلاٌ ليكون التابع هو تابع كسري

مثال :

 

عدد وليس متحولًا ( مجهول)

أمثلة على بعض التوابع الكسرية:

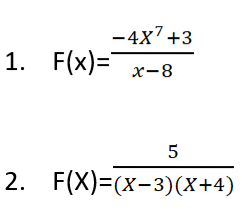
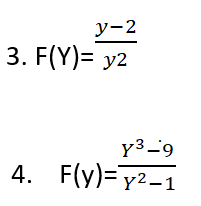
مجموعة تعريف التوابع الكسرية هي:

R/

أي هي مجموعة الأعداد الحقيقية ماعدا ( باستثناء ) القيم التي ينعدم عندها المقام

أمثلة:

لنأخذ الأمثلة السابقة ونوجد مجموعة تعريفها:

 

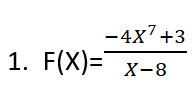
1- الخطوة الأولى للحل هي أن تعدم المقام

 

نعدم المقام :

 

ومنه فإن مجموعة التعريف هي:

{8}/ R

ولنكتبها على شكل المجال فتصبح مجموعة التعريف بالشكل :

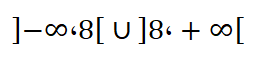
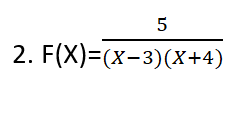
نتبع نفس خطوات الحل في التمرين السابق ، نعدم المقام:

X-3)(X+4)=0)

نلاحظ أن المعادلة هي معادلة من الدرجة الثانية تحل باستخدام خاصة الجداء الصفري:

إما

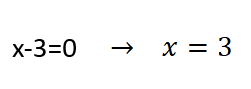
أو

ومنه فإن مجموعة تعريف التابع هي:

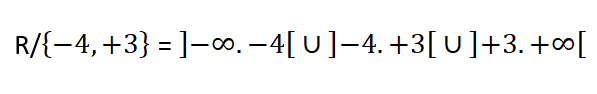
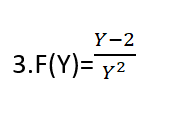
نعدم المقام

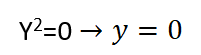
ومنه فإن مجموعة التعريف هي :

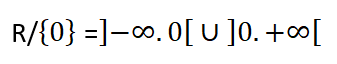
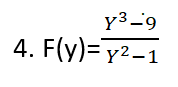
نعدم المقام:

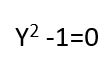
هذه المعادلة معادلة من الدرجة الثانية يجب أن نحللها إلى جداء عوامل من الدرجة الأولى ،ونستنتج أنها أحد المطابقات التربيعية ألا وهي المطابقة:

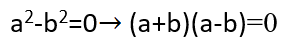
ومنه فإن حل المعادلة هو:

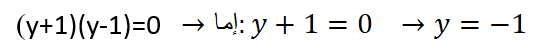
ومنه فإن مجموعة التعريف هي:

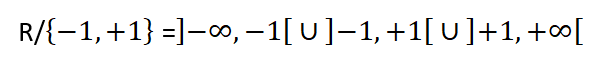
3. التابع الجذري:

يكون التابع جذري إن وجد متحول (مجهول ) تحت الجذر

ومجموعة تعريف التابع الجذري هي ماتحت الجذر أكبر أو يساوي الصفر

لنوضح ذلك في بعض الأمثلة:

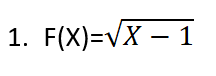
لإيجاد مجموعة تعريفه ننظر إلى ماتحت الجذر ونجعله أكبر أو يساوي الصفر ثمّ نحل المتراجحة :

لنكتب مجموعة التعريف على شكل مجال:

 

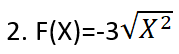
مجموعة تعريفه هي ماتحت الجذر أكبر أو يساوي الصفر أي:

لنكتبها على شكل مجالات فتصبح بالشكل:

وللفائدة أكثر ندعوكم إلى متابعة هذا الفيديو: